Astronomy Calculations:
Excel sheets

Orbit Calculator:

Gravity, Kepler and Newton are exiting physics. Here I have made an orbit calculator. Simplified to only circular orbits.

There are two forces that push and pull radially on a planet in an orbit around the Sun. To get them in equilibrium the forces have to be equal strong. We don't want the planet crash into the Sun or escape and fly away.

Force Equations:
In this case Solar system, simple case when Suns mass is much bigger then any planet mass:

In binary star systems it's common that the masses of the stars are note very different. We can't simplified the equations as much as we did above. The center of mass is somewhere between the stars. Both stars orbit around this point.

Orbital period, tangential speed and common mass center (barycenter)
We need more precise equations:

Put the equations in an Excel sheet like the one below: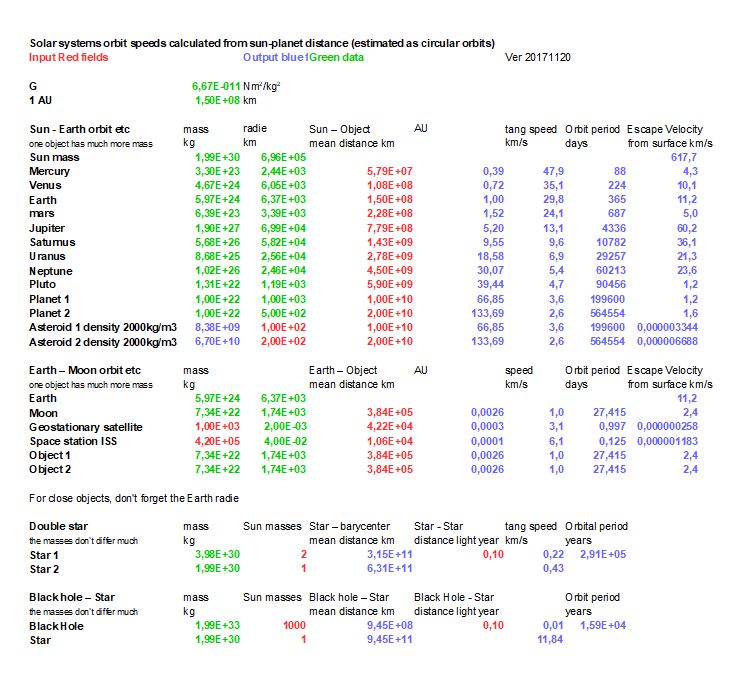

Play around with the figures and help Newton, put in your own planets and objects. You only need the distance between the object to the Sun or the Earth, write it in the red fields.

The escape velocity from Earth is 11.2 km/sec, compare that with ISS station orbital speed above.

Both objects rotate around a common gravity center, but if one of the objects has much more mass it's like that one is still and the other rotate around the heavy one.

• More about gravity and forces:

• Gravity force
  (Gravity, Wiki)
• Centripetal force
  (Centripetal force, Wiki)
• Escape velocity
  (Escape velocity, Wiki)
• Kepler's Laws
  (Kepler's Laws, Caltech)
• Barycenter
  (Barycenter, Wiki)