|
Advertisement / Annons: |
Tutorial:
|
Content: |
1: Introduction Pixel matchingI have spent a lot of time on my new equipment setup to have it as small and low weight as possible. Now I do a calculation how well my camera's pixel match the new 300 mm medium format lens. I only have one camera but it could be interesting to know if it's good or bad. I got inspired from this YouTube video: I have done a lot of other calculations and some of them you find here: Astro calculations 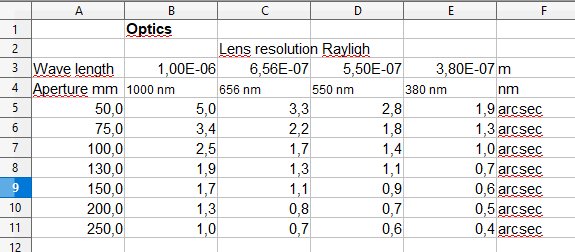
The theoretical resolution of a lens or telescope is related to its opening, the diameter of the front lens or primary mirror. Also which wavelength to observe at is important to plan for. Maybe often the visual spectra that's interesting: from 380 to 660 nm with little extra for the H-Alpha at 656 nm. It could also be exiting to investigate a bit into the IR wavelengths, then it will be a totally different pixel match. Here I have included some examples of wave lengths to compare. More about how the calculations where made at Wikipedia:
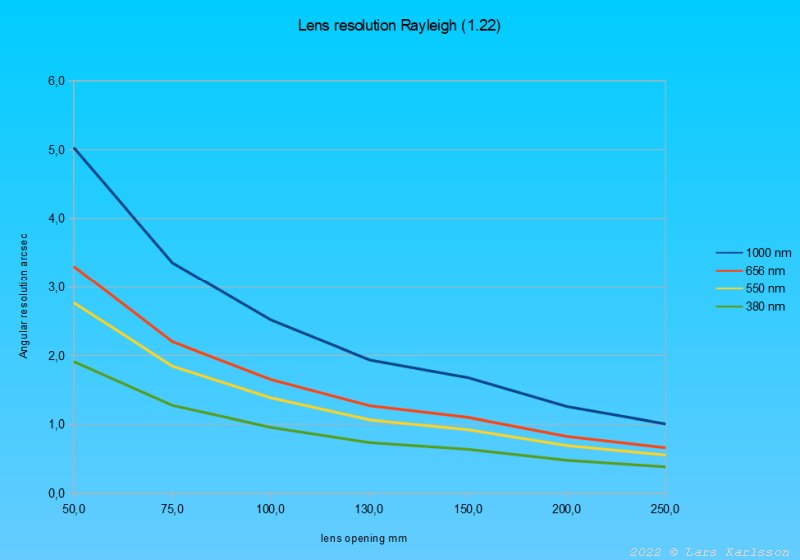
I have a color camera and in the above graph the yellow and red line give information about the resolution. I use the Rayleigh as criteria about the resolution, this is more used for visual I think. But doesn't matter, the resolution limit floats. I have one lens, Pentax 645 300 mm ED IF lens, it has an opening of 75 mm at wide open, f/4. The other is a telescope, TS130, 5.3" APO refractor, 910 mm focal length and 130 mm opening. I use the same camera to both of them, it's a Canon 6D full frame camera, it has the pixel size 6.55 my. It's a color camera and the color pixels are collected in blocks of 4x4, one red, two green and one blue pixel. You can see it like that each color pixel has the twice size, 13.1 my, or with more advanced image processing with Drizzling technic it could be possible to get full resolution of all colors. 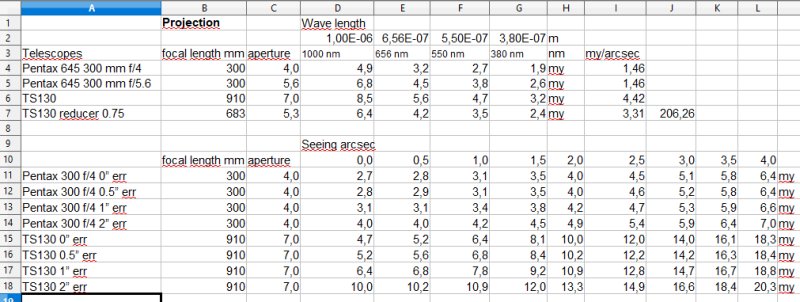
Now we know the resolution and we must know how big the lens project the image on the sensor. In these calculations I have chosen the 550 nm wave length as reference, it's the green color where our eyes are most sensitive. To my telescope I have two field flatteners, one 3" with 1x and another 2.5" with 0.75x. I get the same result from them. The one with 0.75x can only be used for cameras up to APS-H format, the 1X can be used for full frame and then more area are collecting the photons. All camera lenses performs normally better when closing down the aperture, from f/4.0 to f/5.6 is normally found to give the best quality. I plan to use my Pentax lens fully open even if it's a bit softer at that setting. More an experiment to see how much I can do in the pre processing later. 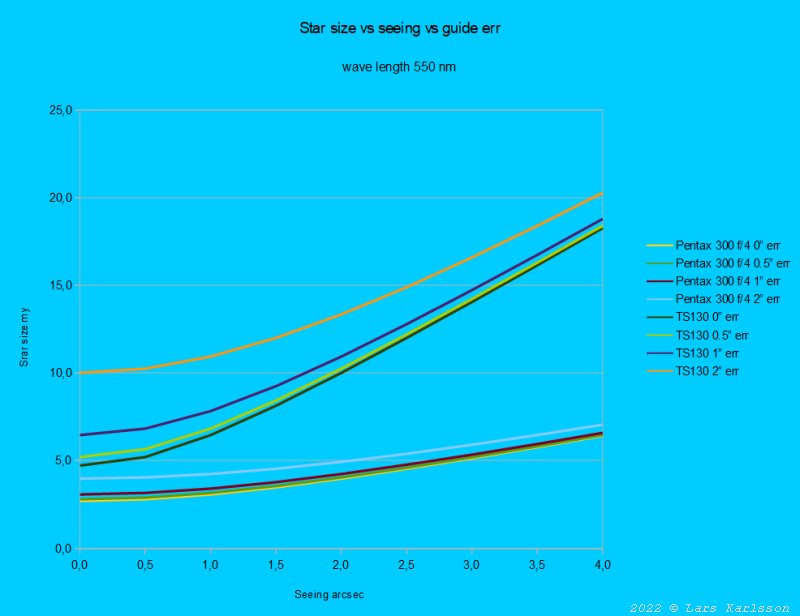
The calculations above are based on the theoretical resolution, here I have added the effect of guiding errors and seeing. In the reality the lens is worse than the theoretical resolution, the seeing disturb and guiding isn't perfect, it makes the stars to be bigger. The upper lines belong to the TS130 telescope, the lower is for the Pentax 300 mm lens. When I use this table I look at the point where seeing is 2", that's very good and doesn't happen often. But when it have this stable atmosphere value I want the camera to be optimized for that. The telescope TS130, when a star size on the sensor is 10 my the optimal pixel size is about half of that, 5 my, the Nyqvist Theorem. It matches my camera's 6.55 my pixel very well. If you find IR wavelength is more interesting the resolution is lower and a camera with big size pixels can be chosen. On the other hand if deep blue or even UV is the main interest smaller pixels is more of interest. The Pentax lens which only has a focal length of 300 mm and have an opening of 75 mm benefit from smaller pixel, 3 my or there about. With this lens I don't aim for highest possible resolution, even the sensitivity is important and then it's good with bigger pixels even if it gets under sampled. There are always compromises that must be done and the budget is not unlimited. The Pentax lens is more for hunting nebulae and the telescope more for galaxies and star clusters.
|
|