Astrofriend's homepage

 www.astrofriend.eu
Share: Twitter Reddit Facebook Gmail Gmail Email
Search Astrofriend's homepage:

Valid CSS!

All pages shall now have been validated

Info Cookies (Kakor) / GDPR

Navigation

Advertisement /
Annons:

Project News

Advertisement / Annons:

Astronomy Calculations

Content:

Bit Resolution Calculator

In old time memories in the computers were expensive. You did everything to keep the need of memory at minimum. Nowadays memories are cheap. When doing image processing on astronomy photos you don't want the data be truncated when you do calculation on them. On example, the average value of 11 and 12 is 11.5, when storing it in a 8-bit format you lose the 0.5 part.

Here are information about some common formats:

Color depth:

But how big bit-depth do we need? Here I have made a calculator that could be of help:

Old astro image processing software like the popular and advanced Iris use signed 16-bit, gives +/- 32000 range. Internally it used 32-bit. Nowadays most software can read and store in 32-bits floating point format. Of this 24-bits are used for the base, the rest, 8-bit is used for the exponent. When I did something more advanced in the 1990s I used Matlab which use 64-bits format in its calculation. But what is the demand of bit-resolution when doing astro image processing?

Note:
This is in theory, in reality you need less, mostly because a lot of noise mask the small part of the rounding errors.

 Panstarrs comet

Type in your data

It start to calculate as soon you change or write new figures in the white or dark red boxes. Do not exceed the maximum number of characters, delete characters if necessary.

Note:
You use the information on your own risk! There can always be a mistake in my equations behind the calculations, check that the result is correct. Let me know if you find something wrong and I try to correct it. Some calculations are very simple done and not correct in the small details.

Bit Resolution Calculator:
This calculation is new and it can be a lot of wrong thinking from me or mistakes in the equations. This calculation is done with integers. But you get the same demand of bit resolution even if you working with average.

As you will notice, each time you double the dynamic or range you need one more bit.

This is one channel image, monochrome image. To a R, G, B image you need three of them.

Fill the table with your data from top to bottom and see how the demand on bit resolution increase for each step.

camera data

    

1, Your cameras bit- depth, common are 8, 10, 12, 14, 16-bits
Camera bit-depth      
= Value Needed bits
6 to 20 bits   int value needed bits

2, HDR, High Dynamic Range?

ISO high / ISO low or Gain high / Gain low
HDR relations
= Value Needed bits
1 to 10, no hdr = 1   int value needed bits

calibration

    

3, Dark calibration

If your subtraction include both dark and bias you should set bias (dark) to = 0,
if you have a separate bias for flat, set bias to = 1.
no = 0, yes = 1      
     
0 or 1      

4, Bias calibration

If you have two different bias, one for dark and another bias for flat, set yes = 2.
no = 0, yes = 1, 2      
     
0, 1 or 2      

5, Number of sub images for each master calibration image
number of sub images   including above  
= Value Needed bits
0 to 100   int value needed bits

6, Flat field calibration (needs a lot of extra precision, bits)

Normal value can be =3 to 5 extra bits if you do flat calibration, if not set to = 0.
no = 0, yes = 1, 2, 3, 4, 5, 6   including above  
= Value Needed bits
0, 1, 2, 3, 4, 5, 6      

stack

    

7, How many images are you plan to stack?
number of images   including above  
= Value Needed bits
1 to 1000   int value total needed bits

image processing

    

8, Plan to do image processing (needs a lot of extra precision, bits)?

Normal value can be =3 to 6 extra bits if you do image processing, if not set to = 0. This part is hard to tell, needs a lot of extra bits, it matters especially if you have low noise data.
no = 0, yes = 1, 2, 3, 4, 5, 6   including above  
= Value Needed bits
0, 1, 2, 3, 4, 5, 6   int value total needed bits

number format

    

9, Plan to use floating point number format? It add 8+1 bits.

Note:
The 32-bit floating point only use 23-bit to store your value in and 1-bit for sign +/-. 7-bit store the exponent and 1-bit for sign +/-.
no = 0, yes = 1   including above  
= Value Needed bits
0 or 1   int value total needed bits

Illustration of bit resolution:

I think there is a need of an illustration of what happens, even for me.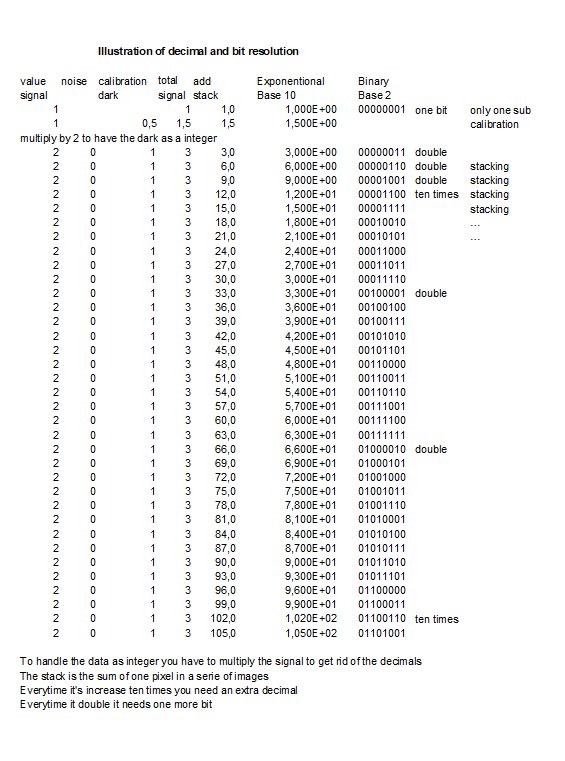

Illustration of bit-resolution

In my calculations I only work with integers to make it easier to follow. When you get rounding errors like 0.5 you have to multiply by 2 to get it back in integer. This double the value and every time you do that you need an extra bit. With stacking, in this case adding them together you need one more extra bit every time the value doubles.

There are situations that are not correct handled, see it like a development project.

Information:

My normal values:

  1. 14-bit rgb camera, Canon 6D, of its 16384 bits resolution 14336 is used for image data
  2. no HDR, I have tried it, then I use ISO 1600 and ISO 400, 1600 / 400 = 4
  3. no dark, use constants instead and then lower the random noise *
  4. no bias, use constants instead and then lower the random noise *
  5. 50 sub images for flat calibration
  6. flat calibration, optics low vignetting, at corner full frame -30%
  7. stack of 60 images
  8. image processing, normally only basic
  9. floating number precision

*
Dithering and median stacking, works good for cameras with low static pattern.

With that input data gives an indication that I need a 35-bit format, 3 bits more then the standard 32-bit floating point. But as said in the beginning, this is in theory, you have a lot of noise that mask the rounding errors. 32-bit floating points format will handle all normal cases.

I normally use the AstroImageJ or Fitswork software, both of them handle 32-bit floating point, here is more information: My Software and equipment

My camera is a Canon 6D and the raw files from it I store as they are .CR2, sometimes if needed I store them as 16-bit fits, .fts or 16-bit TIFF, .tif. Both unsigned integer.

There are more thing, most cameras are nonlinear, to correct for that need some extra precision. Distortion in optics can be corrected too, even this need some extra precision.

After feedback from other people I have added more bits for flat calibration.

It was very interesting to do this calculation, I have just always thought that 32-bit floating point will be enough with a huge margin. Maybe in some extreme rare cases it's not so. It tells me that it could be interesting to do a test with a software that can handle the 64-bit floating point standard. To get any meaning form it I need very high quality images.

In future we maybe will see CMOS cameras with multiple readout, when doing this with different gains you get a HDR image. 16-bit or maybe even 18-bit direct out from the camera.

Go Back to content
Go Back

Advertisement / Annons: